Relevé d'activité radioactive, CPM, 24 heures, 1 relevé par minute
Les premières questions qui viennent à l'esprit en analysant ce type de relevé sont celles-ci : Que signifient ces montagnes Russes ? La radioactivité "naturelle" n'est-elle pas plus ou moins une constante ? Pourquoi les valeurs passent-elles soudainement du simple au quadruple ?
La définition de base : La désintégration radioactive
Tout est poison, rien n'est poison, disait Paracelse. De même, tout est radioactif dans la nature mais rien n'est forcément dangereux, tout est une affaire de concentration, de dose. Ah, si l’œil humain pouvait être sensible à la radioactivité, tout comme le sont les capteurs de certains APN ou caméras numériques, la tâche de détecter des niveaux dangereux - c'est bien l'objectif de la radioprotection : Détecter et protéger des sources radioactives dangereuses - serait bien plus aisée !
Hélas nous devons nous en remettre à des artifices et utiliser des capteurs sensibles aux désintégrations radioactives. Nous sommes donc entourés de radionucléides qui peuvent être "naturels" - le gaz radon est le meilleur exemple connu avec une activité massique très élevée de 5.7*10^15 Bq pour un gramme - mais plus généralement consécutifs à l'activité humaine : Essais d'armes atomiques, sources médicales, accidents et fuites du nucléaire civil...
Notre petit capteur va donc se borner à quantifier les désintégrations à proximité immédiate afin d'estimer si l'environnement présente des dangers ou non, selon des normes sanitaires assez définies mais qui peuvent toutefois se voir modifiées en cas de "force majeure". Ainsi au Japon, les autorités ont-elles relevé la limite sanitaire "d'évacuation" par un facteur de 20 suite à l'accident de Fukushima-Daiichi (données CIPR : 1mSv/an). Il est vrai qu'il y avait sûrement un peu de marge de sécurité mais un facteur de 20, quand même, cela force à réfléchir sur la "normalité" des normes...
Quelques notions d'unité de mesure d'activité radioactive
Le graphe d'activité ci-dessus est exprimé en CPM, c'est-à-dire en désintégrations radioactives par minute (Coups Par Minute). Chaque particule contenant des radioéléments et passant à portée de notre capteur (dans notre exemple un tube Geiger-Müller GMT-02 de fabrication Russe) activera ce dernier par ionisation d'un gaz contenu dans une ampoule. Un petit circuit de détection permettra d'obtenir une estimation sommaire des "coups radioactifs" analysés et enregistrés ensuite par un petit logiciel informatique.
L'unité "basique" de mesure brute d'activité radioactive est le CPS/DPS (Coup/Désintégration par Seconde) qui correspond à 1 Becquerel (Bq). Si l'activité est intense, le Bq / CPS sera vite dépassé et l'on pourra utiliser l'ancienne unité : Le Curie ou Ci (Les unités sont toujours de genre masculin mais il s'agit bien ici de rendre hommage aux travaux sur la radioactivité réalisés par Marie et Pierre Curie) qui vaut 3.7*10^10 Bq et qui correspond plus ou moins à l'activité massique d'un gramme de Radium (226Ra).
Le "bruit de fond" radioactif
Revenons à notre relevé d'activité et à son "bruit de fond" si étonnant au premier abord. La théorie de la radioactivité nous apprend "qu'un noyau radioactif à autant de chances de se désintégrer qu'une autre similaire". C'est la loterie ou plutôt la roulette atomique : A la roulette, les chances simples (Noir/rouge, Pair/Impair...) ont quasiment le même facteur de probabilité de sortie (P = 18 chances sur 37 = 0.486). Pourtant on constate des séries de 10 "rouge", 15 "pair" d'affilée etc. Il n'y a pas de limite théorique à une série, la probabilité de sortie d'un chance simple étant toujours approximativement d'une chance sur deux.
Le même calcul peut s'appliquer à nos désintégrations : Les noyaux de radioéléments sont par définition instables c'est à dire qu'ils finiront tôt ou tard par se désintégrer en provoquant un "Coup" mais il n'existe aucune loi qui définit à quel moment précis tel ou tel noyau radioactif va se rendre à cette "évidence" ; Le seul calcul pouvant nous aider est celui des probabilités et des lois statistiques portant sur un grand nombre d'événements de désintégration.
Imaginons que notre détecteur soit à proximité d'une source émettant en moyenne 100 "méchantes" désintégrations chaque minute soit 100 CPM. Première minute, nous mesurons 100 CPM, la moyenne, exemple "idéal". Deuxième minute, nous mesurons 50 coups soit 50 désintégrations ; Est-ce anormal ? Non car nous aurons relevé 50% de notre moyenne de 100, ou encore 0.5 fois notre moyenne. Troisième minute, 150 CPS, le retard de désintégrations est "rattrapé", nous avons bien 300 désintégrations en 3 minutes soit notre moyenne idéale.
Des exemples de séries de relevés d'activité en CPM
Voici un relevé réel de 120 minutes d'activité (2 heures) sur notre capteur
Attention: Les valeurs ne sont pas celle du graphe en tête d'article !
21, 16, 15, 19, 13, 29, 19, 12, 19, 8,
24, 12, 19, 19, 18, 19, 26, 16, 13, 18,
22, 20, 25, 20, 17, 19, 23, 17, 14, 13,
25, 23, 28, 15, 20, 20, 20, 12, 12, 18,
16, 26, 15, 28, 20, 20, 24, 13, 12, 17,
26, 16, 14, 21, 18, 19, 11, 13, 17, 26,
19, 22, 14, 15, 21, 20, 21, 14, 18, 16,
14, 29, 17, 17, 13, 19, 22, 12, 18, 22,
16, 20, 21, 17, 23, 17, 14, 27, 18, 16,
16, 19, 20, 17, 15, 18, 21, 28, 15, 19,
26, 22, 36, 26, 18, 13, 23, 23, 20, 18,
15, 20, 18, 17, 18, 21, 16, 23, 24, 21,
- R est un Relevé
- Le nombre de Points de mesure P est de 120
- La valeur Faible F est de 8 CPM (m+10)
- La valeur Elevée E est de 36 CPM (m+103)
- La Somme S de nos relevés est de 21+16+15+... = 2268
- La moyenne M est de S / P = 18.9
- La dispersion ou déviation standard SD de notre échantillon est de 4.62 : racine carrée de (S(R(p)-M)/P)
D'après la loi de distribution statistique normale :
- 68.3% des événements (mesures, minutes) seront compris dans l'intervalle M+SD et M-SD soit entre (18.9-4.62)=14.27 CPM et (18.9+4.62)23.52 CPM
- 95.5% des événements (mesures, minutes) seront compris dans l'intervalle M+(2*SD) et M-(2*SD) soit entre 9.66 CPM et 28.14 CPM
- 99.7% des événements (mesures, minutes) seront compris dans l'intervalle M+(3*SD) et M-(3*SD) soit entre 5.04 CPM et 32.76 CPM
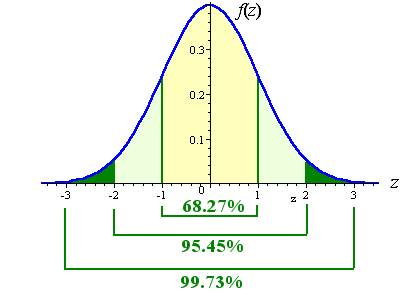
D'après cette loi "Gaussienne", notre relevé de mesure "E" de 36 CPM est au-delà de 3*SD, il est donc considéré comme statistiquement "anormal". Cela ne veut pas dire qu'il ne se produira jamais mais juste qu'il est très peu fréquent et que sa survenue doit amener à se pencher un peu plus sur l'échantillon de mesures. Je dois bien vous avouer maintenant que j'ai un peu "triché" en sélectionnant dans une base de données qui commence à bien se remplir une "anomalie", réelle mais qui ne devrait théoriquement pas "trop" apparaître dans un si petit échantillon de mesures !
La véritable anomalie statistique est-elle ailleurs ?
En revenant sur notre série de 120 mesures effectuées sur une période de 2 heures, on remarquera toutefois que le relevé Elevé "E" de 36 CPM se situe donc "au-delà" de la distribution normale alors que le relevé Faible "F", qui n'est, lui, "que" de 8, rentre à l'intérieur de cette même loi avec une déviation standard d'environ 2.2. Si cette "anomalie" se maintient sur un grand nombre de relevés, ce sera peut-être le signe que les quelques "pics" de radioactivité que j'évoquais dans un précédent article méritent décidément un peu plus d'attention !
Application pratique de la loi de distribution normale à la roulette
Un petit "easter egg" pour les lecteurs qui auront atteint la fin de ce papier sans s'endormir ni changer de site : Savez-vous que la décroissance radioactive trouve une application pratique dans les générateurs aléatoires de jeux de casino ? L'aspect complétement aléatoire de ce type de source de "hasard" est en effet utilisé par plusieurs grands groupes de casinos en ligne pour simuler le "véritable" hasard - ou s'en approchant - fourni aux tables de jeu. Voilà pourquoi je m'amusais à vous parler de roulette et de probabilités un peu plus haut.
Bons relevés à tous et surveillez bien les anomalies : Le signe d'une dissymétrie prolongée entre -SD et +SD pourrait être le marqueur de "quelque chose" dans l'air, qui méritera que l'on s'attarde un peu sur les mesures et leur interprétation, quoiqu'en disent les autorités de tout crin...
Un calculateur en ligne pour calculer vos SD et vos distributions : http://www.calculator.net/ . Vous pouvez retrouver les mesures effectuées en direct sur : http://gen4.dyndns.tv:700/ Attention, machinerie en test, les coupures sont fréquentes ! Votre ISP / FireWall ne doit pas bloquer le port 700 !

La définition de base : La désintégration radioactive
Tout est poison, rien n'est poison, disait Paracelse. De même, tout est radioactif dans la nature mais rien n'est forcément dangereux, tout est une affaire de concentration, de dose. Ah, si l’œil humain pouvait être sensible à la radioactivité, tout comme le sont les capteurs de certains APN ou caméras numériques, la tâche de détecter des niveaux dangereux - c'est bien l'objectif de la radioprotection : Détecter et protéger des sources radioactives dangereuses - serait bien plus aisée !
Hélas nous devons nous en remettre à des artifices et utiliser des capteurs sensibles aux désintégrations radioactives. Nous sommes donc entourés de radionucléides qui peuvent être "naturels" - le gaz radon est le meilleur exemple connu avec une activité massique très élevée de 5.7*10^15 Bq pour un gramme - mais plus généralement consécutifs à l'activité humaine : Essais d'armes atomiques, sources médicales, accidents et fuites du nucléaire civil...
Notre petit capteur va donc se borner à quantifier les désintégrations à proximité immédiate afin d'estimer si l'environnement présente des dangers ou non, selon des normes sanitaires assez définies mais qui peuvent toutefois se voir modifiées en cas de "force majeure". Ainsi au Japon, les autorités ont-elles relevé la limite sanitaire "d'évacuation" par un facteur de 20 suite à l'accident de Fukushima-Daiichi (données CIPR : 1mSv/an). Il est vrai qu'il y avait sûrement un peu de marge de sécurité mais un facteur de 20, quand même, cela force à réfléchir sur la "normalité" des normes...
Quelques notions d'unité de mesure d'activité radioactive
Le graphe d'activité ci-dessus est exprimé en CPM, c'est-à-dire en désintégrations radioactives par minute (Coups Par Minute). Chaque particule contenant des radioéléments et passant à portée de notre capteur (dans notre exemple un tube Geiger-Müller GMT-02 de fabrication Russe) activera ce dernier par ionisation d'un gaz contenu dans une ampoule. Un petit circuit de détection permettra d'obtenir une estimation sommaire des "coups radioactifs" analysés et enregistrés ensuite par un petit logiciel informatique.
L'unité "basique" de mesure brute d'activité radioactive est le CPS/DPS (Coup/Désintégration par Seconde) qui correspond à 1 Becquerel (Bq). Si l'activité est intense, le Bq / CPS sera vite dépassé et l'on pourra utiliser l'ancienne unité : Le Curie ou Ci (Les unités sont toujours de genre masculin mais il s'agit bien ici de rendre hommage aux travaux sur la radioactivité réalisés par Marie et Pierre Curie) qui vaut 3.7*10^10 Bq et qui correspond plus ou moins à l'activité massique d'un gramme de Radium (226Ra).
Le "bruit de fond" radioactif
Revenons à notre relevé d'activité et à son "bruit de fond" si étonnant au premier abord. La théorie de la radioactivité nous apprend "qu'un noyau radioactif à autant de chances de se désintégrer qu'une autre similaire". C'est la loterie ou plutôt la roulette atomique : A la roulette, les chances simples (Noir/rouge, Pair/Impair...) ont quasiment le même facteur de probabilité de sortie (P = 18 chances sur 37 = 0.486). Pourtant on constate des séries de 10 "rouge", 15 "pair" d'affilée etc. Il n'y a pas de limite théorique à une série, la probabilité de sortie d'un chance simple étant toujours approximativement d'une chance sur deux.
Le même calcul peut s'appliquer à nos désintégrations : Les noyaux de radioéléments sont par définition instables c'est à dire qu'ils finiront tôt ou tard par se désintégrer en provoquant un "Coup" mais il n'existe aucune loi qui définit à quel moment précis tel ou tel noyau radioactif va se rendre à cette "évidence" ; Le seul calcul pouvant nous aider est celui des probabilités et des lois statistiques portant sur un grand nombre d'événements de désintégration.
Imaginons que notre détecteur soit à proximité d'une source émettant en moyenne 100 "méchantes" désintégrations chaque minute soit 100 CPM. Première minute, nous mesurons 100 CPM, la moyenne, exemple "idéal". Deuxième minute, nous mesurons 50 coups soit 50 désintégrations ; Est-ce anormal ? Non car nous aurons relevé 50% de notre moyenne de 100, ou encore 0.5 fois notre moyenne. Troisième minute, 150 CPS, le retard de désintégrations est "rattrapé", nous avons bien 300 désintégrations en 3 minutes soit notre moyenne idéale.
Des exemples de séries de relevés d'activité en CPM
Voici un relevé réel de 120 minutes d'activité (2 heures) sur notre capteur
Attention: Les valeurs ne sont pas celle du graphe en tête d'article !
21, 16, 15, 19, 13, 29, 19, 12, 19, 8,
24, 12, 19, 19, 18, 19, 26, 16, 13, 18,
22, 20, 25, 20, 17, 19, 23, 17, 14, 13,
25, 23, 28, 15, 20, 20, 20, 12, 12, 18,
16, 26, 15, 28, 20, 20, 24, 13, 12, 17,
26, 16, 14, 21, 18, 19, 11, 13, 17, 26,
19, 22, 14, 15, 21, 20, 21, 14, 18, 16,
14, 29, 17, 17, 13, 19, 22, 12, 18, 22,
16, 20, 21, 17, 23, 17, 14, 27, 18, 16,
16, 19, 20, 17, 15, 18, 21, 28, 15, 19,
26, 22, 36, 26, 18, 13, 23, 23, 20, 18,
15, 20, 18, 17, 18, 21, 16, 23, 24, 21,
- R est un Relevé
- Le nombre de Points de mesure P est de 120
- La valeur Faible F est de 8 CPM (m+10)
- La valeur Elevée E est de 36 CPM (m+103)
- La Somme S de nos relevés est de 21+16+15+... = 2268
- La moyenne M est de S / P = 18.9
- La dispersion ou déviation standard SD de notre échantillon est de 4.62 : racine carrée de (S(R(p)-M)/P)
D'après la loi de distribution statistique normale :
- 68.3% des événements (mesures, minutes) seront compris dans l'intervalle M+SD et M-SD soit entre (18.9-4.62)=14.27 CPM et (18.9+4.62)23.52 CPM
- 95.5% des événements (mesures, minutes) seront compris dans l'intervalle M+(2*SD) et M-(2*SD) soit entre 9.66 CPM et 28.14 CPM
- 99.7% des événements (mesures, minutes) seront compris dans l'intervalle M+(3*SD) et M-(3*SD) soit entre 5.04 CPM et 32.76 CPM

D'après cette loi "Gaussienne", notre relevé de mesure "E" de 36 CPM est au-delà de 3*SD, il est donc considéré comme statistiquement "anormal". Cela ne veut pas dire qu'il ne se produira jamais mais juste qu'il est très peu fréquent et que sa survenue doit amener à se pencher un peu plus sur l'échantillon de mesures. Je dois bien vous avouer maintenant que j'ai un peu "triché" en sélectionnant dans une base de données qui commence à bien se remplir une "anomalie", réelle mais qui ne devrait théoriquement pas "trop" apparaître dans un si petit échantillon de mesures !
La véritable anomalie statistique est-elle ailleurs ?
En revenant sur notre série de 120 mesures effectuées sur une période de 2 heures, on remarquera toutefois que le relevé Elevé "E" de 36 CPM se situe donc "au-delà" de la distribution normale alors que le relevé Faible "F", qui n'est, lui, "que" de 8, rentre à l'intérieur de cette même loi avec une déviation standard d'environ 2.2. Si cette "anomalie" se maintient sur un grand nombre de relevés, ce sera peut-être le signe que les quelques "pics" de radioactivité que j'évoquais dans un précédent article méritent décidément un peu plus d'attention !
Application pratique de la loi de distribution normale à la roulette
Un petit "easter egg" pour les lecteurs qui auront atteint la fin de ce papier sans s'endormir ni changer de site : Savez-vous que la décroissance radioactive trouve une application pratique dans les générateurs aléatoires de jeux de casino ? L'aspect complétement aléatoire de ce type de source de "hasard" est en effet utilisé par plusieurs grands groupes de casinos en ligne pour simuler le "véritable" hasard - ou s'en approchant - fourni aux tables de jeu. Voilà pourquoi je m'amusais à vous parler de roulette et de probabilités un peu plus haut.
Bons relevés à tous et surveillez bien les anomalies : Le signe d'une dissymétrie prolongée entre -SD et +SD pourrait être le marqueur de "quelque chose" dans l'air, qui méritera que l'on s'attarde un peu sur les mesures et leur interprétation, quoiqu'en disent les autorités de tout crin...
Un calculateur en ligne pour calculer vos SD et vos distributions : http://www.calculator.net/ . Vous pouvez retrouver les mesures effectuées en direct sur : http://gen4.dyndns.tv:700/ Attention, machinerie en test, les coupures sont fréquentes ! Votre ISP / FireWall ne doit pas bloquer le port 700 !

Identificateurs Technorati : mesure d'activité, probabilités appliquées, radioprotection, compteur geiger

Tout est poison, rien n'est poison, disait Paracelse...
Le chimiste allemand Fritz Haber, né en 1868, Prix Nobel de chimie en 1918, a inventé les gaz de combat pendant la première guerre mondiale, puis a travaillé sur les pesticides, des gaz faisant mourir les plantes les insectes les champignons. Il a influencé la toxicologie avec sa "loi de Haber" pour l'évaluation de la toxicité des produits chimiques contaminant notre environnement. La loi dit "Pour chaque gaz de combat, la quantité C présente dans un mètre cube d'air est exprimée en milligrammes et multipliée par le temps T exprimé en minutes qui est nécessaire pour obtenir un effet létal sur l'animal expérimental inhalant cet air. Plus le produit CxT est petit, plus la toxicité du gaz de combat est grande".
Mais savez-vous qu'ensuite, Fritz Haber a constaté que l'exposition à une concentration faible de gaz toxique pendant une longue période a souvent le même effet mortel qu'une exposition à une dose élevée pendant une courte période. Ceci remet totalement en cause le principe de Paracelse dans le domaine de la toxicologie. Et c'est très bizarre, aucune agence chargée d'évaluer les produits chimiques contaminant notre environnement ne parlent de la remarque faite dès le début du XXès par F. Haber. Source : "Notre poison quotidien", Marie-Monique Robin. Arte Editions.
Dans le domaine de l'exposition à la radioactivité artificielle contaminant notre environnement, je n'ai pas de référence d'études abordant ce sujet. Mais il me semble bien trop rapide de mettre en avant le principe de Paracelse comme principe fondamental.
On sait par contre qu'étant donné une quantité donnée de radioactivité relâchée par la centrale de Fukushima, la dilution du nuage diminue le risque de problèmes de santé pour chacun mais ne diminue pas le nombre de problèmes de santé.
Rédigé par : Frédéric Boutet | 22/08/2011 à 22:19
Merci Frédéric, l'article évoquait le principe de mesure de dose de radioactivité sans prétendre rentrer dans les détails. L'application de votre remarque sur les toxicités cumulées de poisons chimiques est prise en compte par les autorités de radioprotection et les praticiens : La RLSS (Relation Linéaire Sans Seuil) dit que de faibles doses de radioactivité cumulées sont équivalentes à une dose unique de la même valeur.
De nombreux spécialistes ne sont pas d'accord avec ce principe et prônent, par exemple, un effet hormésis aux faibles doses mais en attendant un avis scientifique définitif - si cela est possible dans ce domaine -, la RLSS continue d'être la règle. Chaque unité de radiation reçue est donc une unité "superflue" quand cette exposition peut être évitée, bien entendu, et compte tenu d'éventuels avantages induits par cette exposition (médecine nucléaire, imagerie médicale).
Les accidents majeurs sont hélas souvent "déconnectés" de ce principe de précaution car, au Japon par exemple, l'application de la RLSS stricto sensu conduirait à la perte d'une partie importante du territoire de cette "petite" ile très peuplée. Les autorités n'ont donc d'autre choix - à leurs yeux - que de "courir le risque" et de relever les niveaux tolérables annuels pour l'exposition de la population (de 1 à 20 mSv/an).
Bien évidemment, de nombreux scientifiques et médecins ont les yeux rivés sur cette situation qui modifiera probablement la manière d'appréhender les effets des faibles doses en confirmant ou en infirmant la notion de RLSS.
C'est bien là l'un des rares effets positifs que l'on peut espérer tirer de cette catastrophe toujours en cours...
Merci pour votre réaction,
Trifouillax
Rédigé par : Trifouillax | 24/08/2011 à 14:00
Je me demande comment à la fois il peut y avoir :
- une limite annuelle à l'irradiation d'un salarié, et
- le fait que la RLSS prenne en compte le cumul des doses.
Cela me semble contradictoire.
Rédigé par : Frédéric Boutet | 24/08/2011 à 22:05
Un travailleur du nucléaire a un statut un peu différent ne serait-ce que parce qu'il ne côtoiera - en principe - des zones potentiellement très dangereuses qu'au cours de sa vie professionnelle et d'autre part parce qu'il sera sensé être mieux formé, mieux suivi (médicalement) et mieux protégé (équipement) que la population.
D'où l'idée d'étaler les doses maximales des travailleurs sur une vie de travail par définition moins longue qu'une vie moyenne tout court... En considérant que les travailleurs ne seront plus exposés par la suite à la radioactivité "artificielle", ce qui reste à démontrer !
Il y a aussi un petit aspect de "choix" de travailler dans le secteur, si l'on accepte pas les conditions du métier, il existe d'autres filières, à la différence de l'accident qu'on ne choisit que rarement !
En France la dose annuelle "maximale" des travailleurs du nucléaire est fixée à 20 mSv/an sauf exception, une carrière complète de 40 années "au contact" leur conférerait donc une dose équivalente maximale de 800 mSv, à condition d'être exposé chaque année à la dose maximale légale.
Cela peut sembler une limite théorique très élevée mais elle est très rarement voire jamais atteinte en pratique : le bilan de radioprotection IRSN 2009 fait état d'une dose moyenne "externe" de 0.21 mSv/an et par travailleur ce qui équivaudrait à une exposition moyenne de 8 mSv sur une carrière complète et toujours en "externe" :
http://www.irsn.fr/FR/professionnels_sante/actualite/Pages/Bilan_2009_expositions_professionnelles_rayonnements_ionisants.aspx
A noter que la quinzaine de cas annuels dépassant la limite de 20 mSv/an sont majoritairement reportés dans le secteur de la médecine et de l'industrie non nucléaire.
Évidemment, en phase accidentelle gravissime comme au Japon actuellement, le tableau change fondamentalement et les expositions professionnelles "limites" reportées ne sont plus exceptionnelles, elles tendent même à devenir le quotidien d'employés mal formés, mal équipés et mal suivis sur le plan sanitaire. Et encore, ce n'est que la partie "renseignée" des expositions.
La limite maximale a ainsi été relevée après l'accident de Fukushima d'un facteur de 2.5 soit de 100 à 250 mSv/an pour les travailleurs et d'un facteur de 10 à 20 pour la population (20 mSv/an pour les adultes et 10 mSv/an pour les enfants).
De quoi relativiser la relation linéaire "sans seuil" et toutes les belles théories de radioprotection qui ne servent que quand on n'en a pas trop besoin !
Rédigé par : trifouillax | 25/08/2011 à 00:11
Merci pour les explications.
Donc, si la prise en compte du cumul des doses est valable pour le commun des mortels mais inapplicable pour les salariés du nucléaire au motif qu'ils seraient plus informés que les autres, alors je pense qu'on peut parler d'esclaves. D'ailleurs, Annie Thébaud Mony parle de "servitude".
Rédigé par : Frédéric Boutet | 01/09/2011 à 22:49